从一个现象入手
都知道模拟信号经过要想通过计算机处理需要对其进行采样,采样的过程可以看作一个连续函数的离散化,也可以看作信号经过一个电子开关。当然,这样就会引入一个新的参数——采样频率。
假设有一信号,y = cos(0.5x)。我们使用 matlab 对其进行分析:
n = 0:1:300;
x = cos(0.5*pi*n);
w = (0:1:1000)*pi/1000;
X= x* exp(-j).^(n'*w);
magX = abs(X);
plot(w/pi,magX);grid
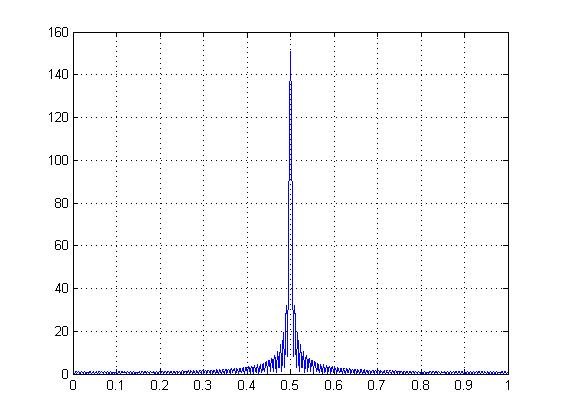
使用 300 点的离散信号,可以看作对模拟信号的采样,自然而然地产生了采样频率 = 300 / 300 = 1 HZ。
从结果上看,响应大部分集中在 0.5pi 的区域,与原函数特性相符。
横轴用 1000 点的离散值逼近连续值,这样的分析方法称为 DTFT——离散时间傅里叶变换。变换特点为时域离散信号变为频域连续信号。
为了简便起见,频率(横轴)的范围是0~pi,会不会有什么东西漏掉了呢?
修改第三行将范围扩大:
w = (0:1:1000)*5*pi/1000;
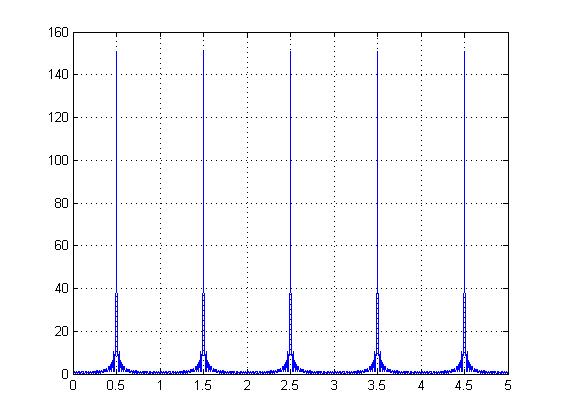
在 1.5pi、2.5pi、3.5pi…地方均出现了响应。为什么呢?
记得之前分析过,采样频率为 1HZ,使用公式 Ω = 2pi * f 可将其转换为角频率 = 1pi。
实际上在频域中,通过采样后的图像为原图像以采样频率进行的周期性延拓。因此会在 0.5 ± N*采样频率(N=0,1,2,..)的地方出现响应。可这是为什么呢?
还是回到时域中来,我们的信号就像一颗颗珠子:
n = 0:1:300;
x = cos(0.5*pi*n);
plot(n,x,'*');
axis([0 50 -2 2]);
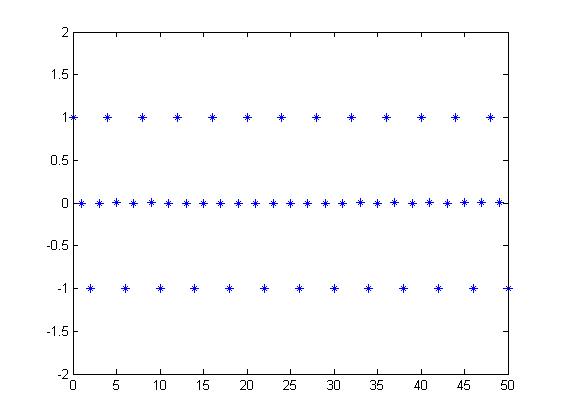
傅里叶分析的目的是观察信号的频率,而我们事先已经知道了这些点是频率为 0.5 pi 的信号,只不过离散处理了。那么我们是否能够用频率为 0.5 pi 的连续信号将其串起来呢?换句话说:想要知道信号的频率,就用此频率的信号去拟合,拟合上了就说明信号符合这一频率。
使用 y = cos(0.5πx) 拟合:
n = 0:1:300;
x = cos(0.5*pi*n);
plot(n,x,'*');
axis([0 50 -2 2]);
hold on;
t = 0:0.01:300;
plot(t,cos(0.5*pi*t),'r');

果不其然,信号完美的落在了红线上。就像串项链一般。
但串法唯一吗?
既然傅里叶分析出了 1.5pi、2.5pi、3.5pi… 的频率,不妨试一试用 cos(1.5πx)、cos(2.5πx)、cos(3.5πx) 串一下:
n = 0:1:300;
x = cos(0.5*pi*n);
t = 0:0.01:300;
subplot(3,1,1)
plot(t,cos(1.5*pi*t),'r');
hold on
plot(n,x,'*');
axis([0 50 -2 2]);
subplot(3,1,2)
plot(t,cos(2.5*pi*t),'r');
hold on
plot(n,x,'*');
axis([0 50 -2 2]);
subplot(3,1,3);
plot(t,cos(3.5*pi*t),'r');
hold on
plot(n,x,'*');
axis([0 50 -2 2]);
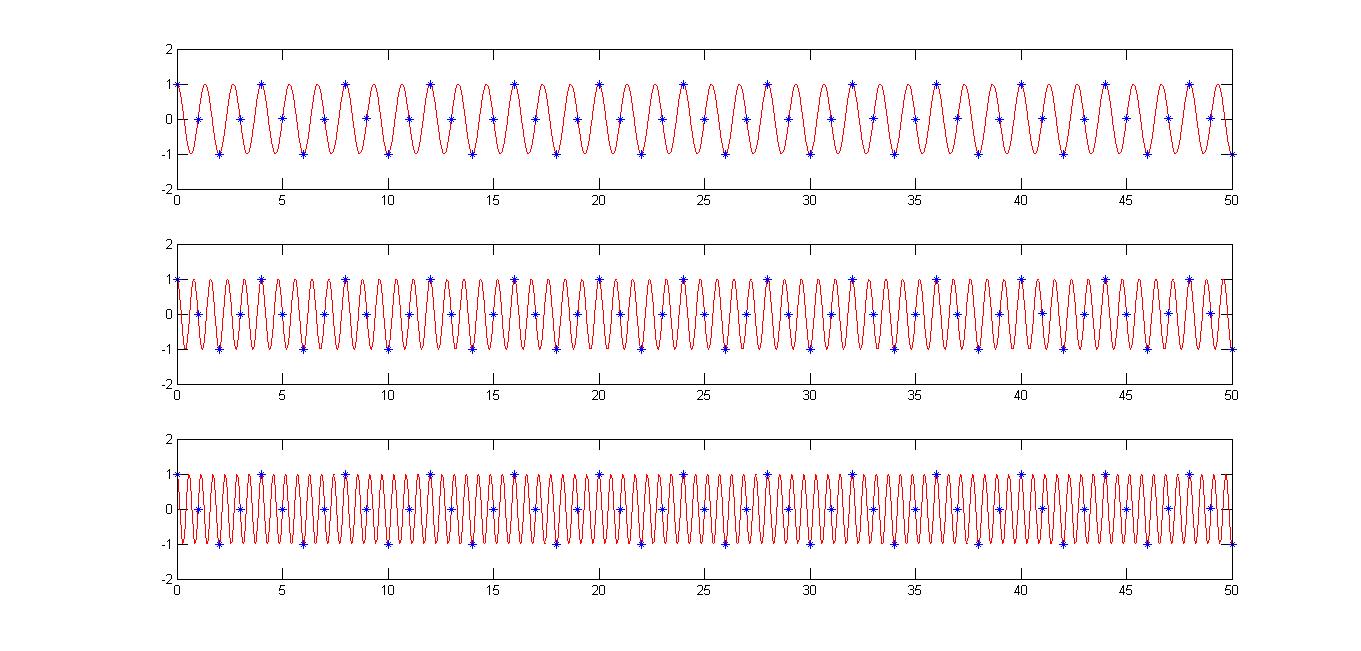
也都很好的被串在了一起。这也就解释了频域分析中出现延拓的现象。通俗来讲:信号离散后使得串法不唯一。
频域采样
连续的东西毕竟不方便使用计算机处理,时域通过采样即可解决。对于频域当然也可如法炮制,这样的变换就是 DFT。其特点为时域离散信号变为频域离散信号。
但这样又引来了新的参数:频域采样点数。幸好频率采样定理说只要频域采样点数大于信号长度即可。
可以用一张图来概括几种分析方法:
参考资料:如何理解离散傅里叶变换及Z变换